Telah dilakukan penelitian optimasi desain
resonator Helmholtz ganda dengan metode algoritma genetika menggunakan MATLAB
7.0. Penelitian dilakukan dengan merancang karakteristik resonator Helmhotz
ganda, kemudian karakteristik tersebut digunakan sebagai fungsi fitness dalam
algoritma genetika. Parameter algoritma genetika divariasi untuk mendapatkan
fitness terbaik dan dianalisa.
Hasil analisa menunjukkan bahwa parameter
terbaik untuk frekuensi (50, 150, 250, 350, 450, 550, 650, 750, 850, 950)Hz
adalah Grefenstette(2) (PopSize=80, Pc=045, Pm=0,01), dan desain resonator
Helmholtz ganda terbaik untuk frekuensi tersebut berturut-turut adalah ((V=0,01159m3, L=0,01574m, Sb =0,00032m2, S=0,00281m2),
(V=0,00351m3, L=0,00414m, Sb =0,00085m2, S=0,00204m2), (V=0,00145m3,
L=0,00020m, Sb =0,00086m2, S=0,00162m2), (V=0,00044m3, L=0,01957m, Sb =0,00086m2, S=0,00160m2), (V=0,00044m3, L=0,00082m, Sb =0,00087m2, S=0,00163m2), (V=0,00018m3, L=0,02137m, Sb =0,00090m2, S=0,00160m2), (V=0,00018m3, L=0,00457m, Sb =0,00079m2, S=0,00163m2), (V=0,00013m3,
L=0,00520m, Sb =0,00082m2, S=0,00237m2), (V=0,00009m3, L=0,01293m, Sb =0,00090m2, S=0,00160m2), (V=0,00005m3, L=0,02457m, Sb=0,00067m2, S=0,00160m2)).
- Banyaknya kasus kebisingan yang bisa mengganggu kesehatan, sehingga muncullah alat penyaring bunyi [1], salah satunya resonator helmholtz.
- Resonator Helmholtz ganda merupakan suatu resonator bercabang yang mempunyai rongga tertutup pada cabangnya yang disusun sejajar secara paralel[2].
- Diterapkan Algoritma Genetika untuk mengoptimasi desain resonator Helmholtz ganda tersebut.
- Tujuannya agar bisa mendapatkan rancangan desain resonator Helmholtz ganda terbaik dengan sifat transmisinya.
- Permasalahan yang dibahas dibatasi dengan anggapan seluruh energi diserap jedalam resonator tanpa adanya kerugian viskositas.
- Tahapan Perancangan Sistem
- Parameter Optimasi dan Variabel input/output
- Ukuran Populasi (PopSize)
- Probabilitas Pindah Silang (Pc)
- Probabilitas Mutasi (Pm)
- Jumlah generasi (makgen)
- Fitness threshold (fthreshold)
- Frekuensi (f)
- Kecepatan bunyi (c)
- Fungsi Fitness
- Model matematika dari koefisien transmisi resonator helmholtz ganda.
- Optimasi dengan batasan (constrained optimization)
- Membuat program GA
- Prosedur Penelitian
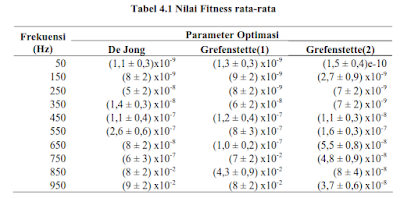
- Dari rentang frekuensi 20-1000 Hz, diambil 10 sampel frekuensi (50, 150, 250, 350, 450, 550, 650, 750, 850, 950) Hz untuk mengecek kelebihan masing-masing parameter optimasi dan sekaligus menunjukkan keberhasilan program optimasi.
- Parameter optimasi (tabel 1.2) akan dicobakan ke masing-masing frekuensi, dan diulang masing-masingnya sebanyak 50 kali.
- Penilaian terbaik ditandai dengan fitness mencapai optimal (mendekati 0).
- Perancangan Optimasi
- Fungsi Fitness
Dalam penelitian ini, dipilih penjabaran
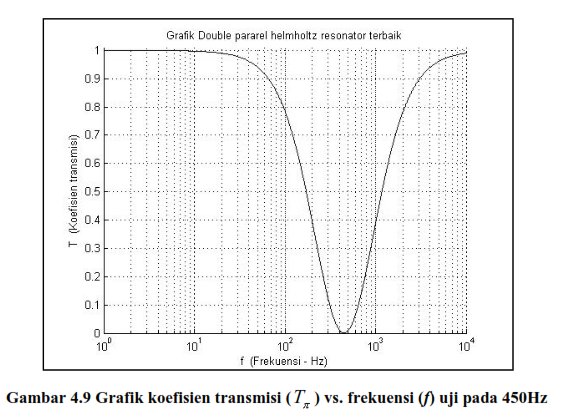
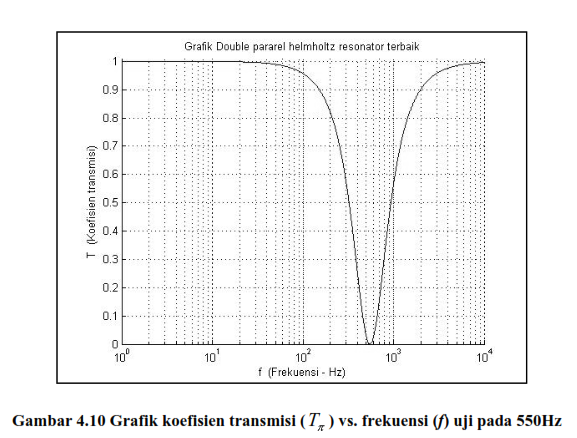
resonator Helmholtz ganda dalam model matematika koefisien transmisi ( Tπ ) sebagai fungsi fitnessnya. Kelebihan dari koefisien transmisi ( Tπ ) adalah kesederhanaannya dalam rumus matematikanya, sehingga tidak begitu
rumit bila dijabarkan kembali ke dalam fungsi fitness algoritma genetika.
- Teknik Algoritma Genetika Standar
- Pertama dibangkitkan bilangan random dari 0 sampai dengan 1 sebagai bentuk dari matriks [populasi, jumlah gen].
- Bilangan random tersebut dibulatkan jadi 0 jika <0.5 dan dibulatkan ke 1 jika >0.5, sehingga menjadi bilangan biner.
- Setelah inisialisasi populasi selesai, dilakukan proses evolusi (gambar 4.2), yang dimulai dengan mendekodekan kromosom kedalam fungsi fitness, dan menghasilkan nilai fitness.
- Dari nilai fitness didapatkan variabel output yang dicari, dan nilai tersebut di encode ke dalam bentuk kromosom biner kembali
- Kromosom biner hasil encoding dicocokkan apakah sudah mencapai optimasi/threshold atau belum, jika sudah, program akan berhenti, jika belum maka dilakukan proses reproduksi.
- Tahap pertamanya, mengkopi kromosom terbaik dari setiap populasi (elitisme)
- Dilakukan proses pemilihan orang tua dengan roulette wheel selection.
- Proses reproduksi akan terus berlangsung dan beberapa gen akan mengalami mutasi.
- Proses selanjutnya mengganti generasi lama dengan baru secara menyeluruh.
- Generasi baru hasil general replacement dievaluasi, jika optimasi tercapai, maka program berhenti, jika belum maka proses general optimation akan terus berulang sampai tercapai optimasi.
- Hasil Simulasi
Dari tabel dapat disimpulkan bahwa nilai fitness semakin naik untuk frekuensi semakin besar. Terutama mulai frekuensi 750Hz ke atas, parameter De Jong dan Grefenstette(1).
Pola seperti itu terbentuk berhubungan dengan karakteristik masing-masing parameter berkaitan dengan ruang solusi.
Sehingga untuk menguji optimasi pada frekuensi antara 20Hz – 1000 Hz, parameter optimasi terbaik yang dapat digunakan adalah parameter Grefenstette(2) karena nilai fitness yang didapatkan tidak jauh fluktuasinya.
- Kesimpulan
- Tanpa memerlukan perhitungan matematika yang rumit dan waktu yang lama, algoritma genetika menjadi lebih mudah untuk digunakan sebagai metode optimasi.
- Parameter algoritma genetika terbaik untuk penyaring bunyi pada frekuensi antara 20Hz – 1000Hz yang teramati dalam penelitian ini adalah parameter optimasi Grefenstette(2). Dimana ukuran populasi (popsize) =80, peluang pindah-silang (Pc) = 0,45 dan peluang mutasi (Pm) = 0,01.
- Untuk dimensi resonator helmholtz ganda terbaik dilihat pada tabel berikut,
- Saran
Pengecekan parameter algoritma genetika lebih banyak lagi, untuk mendapatkan hasil yang benar-benar akurat.
Dibuat tampilan program yang siap pakai (plug and play). Sehingga memudahkan setiap peneliti / student dalam penggunaan dan pembelajaran optimasi.
Berkoordinasi dengan provider untuk memperoleh parameter yang sesuai dengan standar.
- Source Code (click here)
- Video Simulasi Program (click here)















Tidak ada komentar:
Posting Komentar